ディバイダーを使いますか? [試験対策]
ディバイダーは、天気図上で擾乱などの移動距離を測定したり、移動速度を算出するのに用います。もちろん定規でも同じことができます。
ディバイダーの利用には一長一短があるので、本番で用いるかどうかは本文を読んでからご自身で判断してください。
【注意】
ディバイダーなどの用具は普段から使い慣れていることが大切です。慣れていない状態で本番で使うのは時間のロスや間違いにつながります。
使い方はいたってシンプルです。2地点間の距離を測定するには以下のステップを踏みます。
では、順を追って説明していきます。
①ディバイダーを開いて、2本の針をそれぞれの地点に当てます。
特に問題はないと思います。先に一端を合わせてから、もう一端を合わせるようにディバイダーの足を開きます。
ディバイダーの針は紙に穴があくほどには尖っていないので、比較的真上から合わせないと針がズルッと滑ってしまいます。
天気図上で低気圧の中心は低気圧を表す「L」字の重心にあるので、ここにディバイダーの一端を持ってきます。
② ディバイダーの開いている間隔を、経度線を物差しにして度数で測ります。
ディバイダーの針の開いた間隔が距離を表しますが、このままでは距離にはなりません。物差しにあてて距離を測る必要があります。
ここで物差しに使うのが、天気図上を南北に走っている経度線です。ディバイダーを開いたまま東経40度線まで持ってきます。そして最も近い緯度線との交差にディバイダーの一端を合わせ、もう一端を経度線上に置きます。
ディバイダーの開きが経度線上で何度分に相当するかを目分量で読み取ります。上の例では「8度」と読むことができます。後ほど「出題事例」でも紹介するように、ここで読み取る際に誤差が生じる可能性があります。
目分量ではなく定規で測っても良いのですが、これだと手間が増えてディバイダーを使う意味が全くなくなります。
距離換算するには必ず経度線(南北の線)に当てます。地球儀を見ると分かりますが、経度線は必ず北極と南極を通るので1度の距離はどこで測っても同じです(注)。緯度線は緯度に応じて1度の距離が変わってくるので、物差しとして使うことができません。
(注)天気図はポーラーステレオ図法で描かれているので、厳密には異なります。
③ ②で測った度数を海里もしくはkmなどに換算します。
距離を求めるには、②で求まった度数を60倍すると海里(NM)になります。あるいは、度数に111.1を乗じるとキロ数になります。
移動速度(ノット)は1時間あたりの移動海里数なので、12時間の移動速度は度数を5倍(=60÷12)で求まります。
次の関係式を覚えておきましょう。
②で読み取ったの「8度」を距離に換算します。
8度×60(NM/度)=480(NM)
=480(NM)×1.852(km/NM)
=889(km)
この距離を12時間で移動した場合、移動速度は次により求まります。
8度×60(NM/度)÷12(時間)=40(ノット)
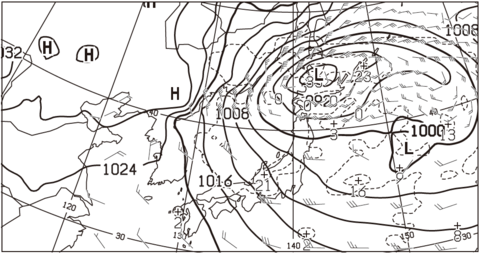
図7(中)に、図6(中)の低気圧の中心を写し取り赤い×をつけます。
次に赤い×と12時間後の低気圧中心(L字の重心)の間隔をディバイダーで測ります。
ディバイダーの開きを経度線で測ります。
開き具合が緯度40度線と50度線で示される10度のほぼ1/4に相当しているので、「2.5度」と読み取ります。
これを12時間の移動速度に換算します。
2.5×60(NM)÷12(時間)=12.5(ノット)
1ノット刻みで答えよとの指定があるので、四捨五入して13(ノット)を得ます。
センターの解答例は「12ノット」であり、13ノットは許容されていません。
正解を得られなかったのは、ディバイダーの開きを2.5度と読み取ったからです。正解を得るにはディバイダーの開きを2.3もしくは2.4と読み取らないといけません。
経度線でコンマ1度レベルまで読み取ることができますか?
ちなみに「1度=60分」ですから、正しくは1/60まで読み取らないといけないことになります。
いずれにしても、私にはできません。
私はディバイダーを使わずに受験しましたが、合格できました。当時は使い方をよく知らなかったということもありますが、定規でも全く不足は感じませんでした。
ディバイダーにしろトレーシングペーパーにしろ、使う道具が増えてくると時間ロスが増えるように思います。
本稿をまとめるにあたりディバイダーを試してみましたが、次の3点がとても気になりました。
ササッと概算値を出すには良いツールだと思いますが、試験では使わなくて正解だったと思います。
あなたならどうしますか?

人気ブログランキングへ
ディバイダーの利用には一長一短があるので、本番で用いるかどうかは本文を読んでからご自身で判断してください。
【注意】
ディバイダーなどの用具は普段から使い慣れていることが大切です。慣れていない状態で本番で使うのは時間のロスや間違いにつながります。
今回のポイント
・移動距離や速度の簡易算出に適するが、誤差が生じやすい。
・使い方に自信がなければ、本番では使わないこと。定規でも十分こと足りる。
・使い方に自信がなければ、本番では使わないこと。定規でも十分こと足りる。
ディバイダーの使用原理
使い方はいたってシンプルです。2地点間の距離を測定するには以下のステップを踏みます。
① ディバイダーを開いて、2本の針をそれぞれの地点に当てます。
② ディバイダーの開いている間隔を、経度線を物差しにして度数で測ります。
③ ②で測った度数を海里もしくはkmなどに換算します。
② ディバイダーの開いている間隔を、経度線を物差しにして度数で測ります。
③ ②で測った度数を海里もしくはkmなどに換算します。
では、順を追って説明していきます。
①ディバイダーを開いて、2本の針をそれぞれの地点に当てます。
特に問題はないと思います。先に一端を合わせてから、もう一端を合わせるようにディバイダーの足を開きます。
ディバイダーの針は紙に穴があくほどには尖っていないので、比較的真上から合わせないと針がズルッと滑ってしまいます。
天気図上で低気圧の中心は低気圧を表す「L」字の重心にあるので、ここにディバイダーの一端を持ってきます。
② ディバイダーの開いている間隔を、経度線を物差しにして度数で測ります。
ディバイダーの針の開いた間隔が距離を表しますが、このままでは距離にはなりません。物差しにあてて距離を測る必要があります。
ここで物差しに使うのが、天気図上を南北に走っている経度線です。ディバイダーを開いたまま東経40度線まで持ってきます。そして最も近い緯度線との交差にディバイダーの一端を合わせ、もう一端を経度線上に置きます。
ディバイダーの開きが経度線上で何度分に相当するかを目分量で読み取ります。上の例では「8度」と読むことができます。後ほど「出題事例」でも紹介するように、ここで読み取る際に誤差が生じる可能性があります。
目分量ではなく定規で測っても良いのですが、これだと手間が増えてディバイダーを使う意味が全くなくなります。
距離換算するには必ず経度線(南北の線)に当てます。地球儀を見ると分かりますが、経度線は必ず北極と南極を通るので1度の距離はどこで測っても同じです(注)。緯度線は緯度に応じて1度の距離が変わってくるので、物差しとして使うことができません。
(注)天気図はポーラーステレオ図法で描かれているので、厳密には異なります。
③ ②で測った度数を海里もしくはkmなどに換算します。
距離を求めるには、②で求まった度数を60倍すると海里(NM)になります。あるいは、度数に111.1を乗じるとキロ数になります。
移動速度(ノット)は1時間あたりの移動海里数なので、12時間の移動速度は度数を5倍(=60÷12)で求まります。
次の関係式を覚えておきましょう。
緯度1度の距離=60NM (NM: nautical mileは海里のこと)
60NM=10,000km÷90度=111.1km(1NM=1.852km)
60NM=10,000km÷90度=111.1km(1NM=1.852km)
②で読み取ったの「8度」を距離に換算します。
8度×60(NM/度)=480(NM)
=480(NM)×1.852(km/NM)
=889(km)
この距離を12時間で移動した場合、移動速度は次により求まります。
8度×60(NM/度)÷12(時間)=40(ノット)
出題事例
図6(中)で北海道付近に予想される低気圧について、その後12時間の移動の速さ(1ノット刻み)を答えよ。
(第46回実技2、問2(2)一部改変)
図6(中)地上気圧・降水量・風24時間予想図
解答例
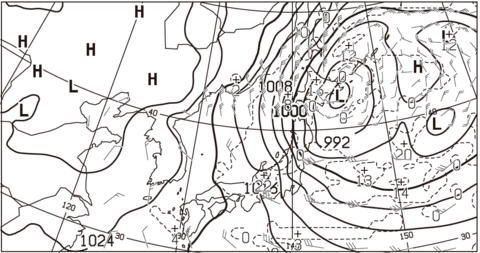
図7(中)に、図6(中)の低気圧の中心を写し取り赤い×をつけます。
次に赤い×と12時間後の低気圧中心(L字の重心)の間隔をディバイダーで測ります。
ディバイダーの開きを経度線で測ります。
開き具合が緯度40度線と50度線で示される10度のほぼ1/4に相当しているので、「2.5度」と読み取ります。
これを12時間の移動速度に換算します。
2.5×60(NM)÷12(時間)=12.5(ノット)
1ノット刻みで答えよとの指定があるので、四捨五入して13(ノット)を得ます。
考察
センターの解答例は「12ノット」であり、13ノットは許容されていません。
正解を得られなかったのは、ディバイダーの開きを2.5度と読み取ったからです。正解を得るにはディバイダーの開きを2.3もしくは2.4と読み取らないといけません。
経度線でコンマ1度レベルまで読み取ることができますか?
ちなみに「1度=60分」ですから、正しくは1/60まで読み取らないといけないことになります。
いずれにしても、私にはできません。
最後に
私はディバイダーを使わずに受験しましたが、合格できました。当時は使い方をよく知らなかったということもありますが、定規でも全く不足は感じませんでした。
ディバイダーにしろトレーシングペーパーにしろ、使う道具が増えてくると時間ロスが増えるように思います。
本稿をまとめるにあたりディバイダーを試してみましたが、次の3点がとても気になりました。
・1ノット刻みを求められる場合は、読み取り精度に難がある。
・開脚角度が小さいとディバイダーが紙面の上を滑ってしまいイライラする。
・1NM=1.852kmの換算値を忘れるリスクがある。
・開脚角度が小さいとディバイダーが紙面の上を滑ってしまいイライラする。
・1NM=1.852kmの換算値を忘れるリスクがある。
ササッと概算値を出すには良いツールだと思いますが、試験では使わなくて正解だったと思います。
あなたならどうしますか?
人気ブログランキングへ
計算問題はここに注意しよう [試験対策]
計算問題毎回のように出題されています。数字の扱い方に慣れておきましょう。
観測装置やグラフの読み取りには、必ず誤差が含まれます。誤差の大きい数値と小さい数値が混在している場合は、あまり細かいところに気を使っても労力のムダです。
そこで有効数字という考え方を用いて、一定のルールに従って数値の処理を行います。有効数字とは最下位の桁に誤差を含む数値のことです。
結論から言うと、気象予報士試験では有効数字の考えが徹底されていません。計算問題では与えられた数値をそのまま使って計算すれば問題ありません。解答でもある程度の数値の幅が許容されています。
しかし以下の2点だけは頭に入れておきましょう。
グラフの読み取りでは、軸で与えられた最小目盛の1/10まで読み取ります。そこまでは目分量で読むことができるからです。
試験でよく出される問題に、「降水量の時系列図から、最大降水量を読み取り答えよ。」があります。
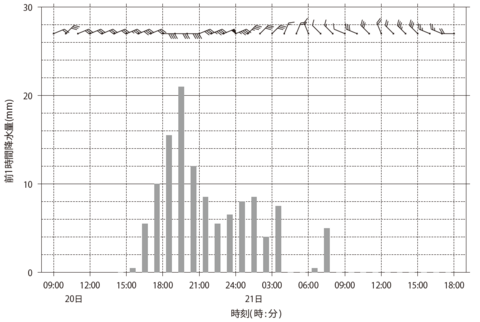
こちらは第45回実技2、問3(3)で出題された地上風・降水量の時系列図です。
前1時間降水量は縦軸で表されています。最小目盛は2mmなので、その1/10の0.2mmまでを読み取ります。
例えば、
19時までの前1時間 ・・・15.6mm(15.5mm)
20時までの前1時間 ・・・21.0mm(21.0mm)
21時までの前1時間 ・・・12.0mm(12.0mm)
と読み取ることができます。
【補足】
上記の読み取り値で()内は「模範解答と解説」(東京堂出版)の解説に示された読み取り値です。これだと最小目盛の1/20まで読んでいることになります。そもそも与えられた図の目盛は定規で読み取っても4.5mm程度であり、これ自体誤差を含んでいます。したがって、1/20まで読み取る必要はありません。
有効数字はちゃんとやろうとすると少し面倒ですが、試験対策上は「求められている桁数より、途中の計算では1桁分だけ桁数の大きな数で行う」ことを覚えておきましょう。
例えば、「小数点第1位を四捨五入して答えよ」とあれば、途中の計算は小数点第2位までで行います。
ただし、小数点の掛け算・割り算で混乱が発生することがあります。次の問題を見てください。
①の解説:
風速の最小目盛は1(m/s)なので、0.1(m/s)まで読み取ります。
最大瞬間風速は0時50分の21.9(m/s)と読み取れるので、「1(m/s)刻み」との指示に従い22(m/s)が答えになります。
②の解説:
この時の平均風速も0.1(m/s)まで読み取り、8.9(m/s)と読み取ります。
さて、瞬間風速の平均風速に対する比を計算するときに、どの数値を使えば良いのでしょうか。
瞬間風速は21.9もしくは22、平均風速は8.9もしくは9が考えられます。①と②で有効数字が揃っていないのでこの混乱が生じます。
②では「小数第1位で答えよ」とあるので、
・計算に使う数値も小数第1位のものを使う
・途中の計算は小数第2位まで行う
・最後に小数第2位を四捨五入する
とするのが最善策です。
21.9÷8.9=2.46 →2.5となります。
ちなみに、①で1(m/s)刻みとしているので、センター発表の解答例では 22÷9=2.4 も許容されています。
センター発表解答例:
瞬間風速の平均風速に対する比: 2.5(2.4)
端数処理とは数値を丸めることで、計算結果を最大有効桁位にするのに用いられいます。
試験では「四捨五入して答えよ」のような指示に従えば良いだけです。一般的な端数処理は四捨五入ですが、過去には「二捨三入」が出題されたことがあります。
本番でびっくりしないように慣れておきましょう。
過去4回分(第45回〜第48回)の試験問題を分析すると、四捨五入の問題は次の二つに大別できます。
①小数第1位を四捨五入して、整数で答えさせる。
問題文としては「小数第1位を四捨五入して整数で答えよ」「四捨五入により整数値で答えよ」「四捨五入により1mm刻みで答えよ」というものです。
求める数値は整数なので、途中の計算は小数第1位まで計算し、最後に小数第1位を四捨五入して整数にします。
例) 43.5 →43
②四捨五入により小数第1位までの数値で答えさせる。
問題文としては、そのまま「四捨五入により小数第1位までの数値で答えよ」です。
小数点以下第1位までの数値を求めるので、途中の計算は小数第2位までで行います。最後に小数第2位を四捨五入して小数第1位までの数値にします。
例) 43.54 →43.5
最小の位の数字を「0」か「5」に揃えるために用いられます。
この処理から「二捨三入・七捨八入」とも呼ばれます。
分かりにくいので、具体例で見てみましょう。
例)「41から50までの整数を二捨三入しなさい」
答) 41、42 → 40
43、44、45、46、47 → 45
48、49、50 → 50
降水量の時系列図(ここでは省略)から最大3時間降水量は48mmもしくは49mmと読み取ることができます。
いずれの数値でも、1桁目を七捨八入をして50mmとなります。
この前の問題で
地点a: 気温 16.0℃、 混合比 13(g/kg)
地点b: 気温 16.0℃、 混合比 7(g/kg)
と求まっています。
有効数字は3桁として仮温度を求めます。
地点a: T=16.0+0.18×13=18.34 →18.3(小数第2位を四捨五入)
地点b: T=16.0+0.18×7=17.26 →17.3(小数2位を四捨五入)
小数第1位を二捨三入して、Ta=18.5、Tb=17.5 を得ます。
上記では小数第2位を四捨五入してから小数第1位を二捨三入するというステップを踏みました。では、小数第2位を切り捨てて小数1位を二捨三入するとどうなるでしょうか。センター発表の正解例では許容範囲になっています。
地点a: 18.34 →18.3(小数第2位を切り捨て) →18.5(小数第1位を二捨三入)
地点b: 17.26 →17.2(小数第2位を切り捨て) →17.0(小数第1位を二捨三入)
センター発表解答例:
地点a: 18.5(18.0)
地点b: 17.5(17.0、18.0)
そもそもですが・・・、本番の試験で計算間違いは絶対に避けなければなりません。そのためには日頃から、間違い防止を意識した計算を実践しましょう。
まず、次の例題を解いてみてください。
すんなり回答できなかったという方は、かけ算対策をすべきです。本番では検算をしている余裕はありません。一回で確実に計算できるようにしましょう。
答えは次の通りです。
①計算は大きな字で、はっきりと書く
計算に時間をかけたくないので、用紙の隅の方に、まるで悪いことでもしているかのように書いていませんか?走り書き程度だと字がはっきりしないし、桁上がりなどを間違える可能性が高まります。
②縦の列を揃えて書くように意識する
縦の列が揃っていないと、計算の最後に同じ桁の数字を足す時に間違えが発生します。意識して列を揃えるようにします。
③繰り上がりの数字を書く
下の写真のように、繰り上がる数字を忘れないようにメモっていくやり方です。すでに実践している人も多いかと思います。
④新しい計算法を習得する
世の中にはいろんな計算法があります。「インド式」「レンガ筆算」「繰り上がり分離法」などで検索すると出てきます。いずれも③の変形法で、繰り上がる数字を明示的に書くものです。最後の足し算が長くなるというデメリットがあります。
国が異なれば計算法も異なります。気象の勉強を忘れて、計算法にのめり込みすぎないように注意!

人気ブログランキングへ
今回のポイント
・グラフの読み取りは最小目盛の1/10までを読む。
・小数点の計算は、求められる結果より一桁多い桁数で計算する。
・四捨五入だけではなく、「二捨三入・七捨八入」にも慣れておく。
・筆算は大きな字ではっきりと、縦の列を揃えて書く。
・小数点の計算は、求められる結果より一桁多い桁数で計算する。
・四捨五入だけではなく、「二捨三入・七捨八入」にも慣れておく。
・筆算は大きな字ではっきりと、縦の列を揃えて書く。
有効数字に気をつけろ!
観測装置やグラフの読み取りには、必ず誤差が含まれます。誤差の大きい数値と小さい数値が混在している場合は、あまり細かいところに気を使っても労力のムダです。
そこで有効数字という考え方を用いて、一定のルールに従って数値の処理を行います。有効数字とは最下位の桁に誤差を含む数値のことです。
結論から言うと、気象予報士試験では有効数字の考えが徹底されていません。計算問題では与えられた数値をそのまま使って計算すれば問題ありません。解答でもある程度の数値の幅が許容されています。
しかし以下の2点だけは頭に入れておきましょう。
グラフの読み取り
グラフの読み取りでは、軸で与えられた最小目盛の1/10まで読み取ります。そこまでは目分量で読むことができるからです。
試験でよく出される問題に、「降水量の時系列図から、最大降水量を読み取り答えよ。」があります。
こちらは第45回実技2、問3(3)で出題された地上風・降水量の時系列図です。
前1時間降水量は縦軸で表されています。最小目盛は2mmなので、その1/10の0.2mmまでを読み取ります。
例えば、
19時までの前1時間 ・・・15.6mm(15.5mm)
20時までの前1時間 ・・・21.0mm(21.0mm)
21時までの前1時間 ・・・12.0mm(12.0mm)
と読み取ることができます。
【補足】
上記の読み取り値で()内は「模範解答と解説」(東京堂出版)の解説に示された読み取り値です。これだと最小目盛の1/20まで読んでいることになります。そもそも与えられた図の目盛は定規で読み取っても4.5mm程度であり、これ自体誤差を含んでいます。したがって、1/20まで読み取る必要はありません。
小数点の計算
有効数字はちゃんとやろうとすると少し面倒ですが、試験対策上は「求められている桁数より、途中の計算では1桁分だけ桁数の大きな数で行う」ことを覚えておきましょう。
例えば、「小数点第1位を四捨五入して答えよ」とあれば、途中の計算は小数点第2位までで行います。
ただし、小数点の掛け算・割り算で混乱が発生することがあります。次の問題を見てください。
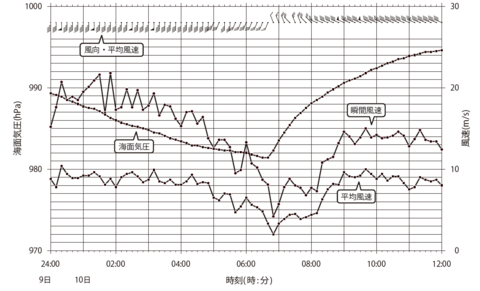
気象要素の時系列図を見て次の問いに答えよ。
①瞬間風速が最大となった時刻(10分刻み)とその風速(1m/s刻み)を答えよ。
②その時刻における瞬間風速の平均風速に対する比を四捨五入により小数第1位までの数値で答えよ。
①瞬間風速が最大となった時刻(10分刻み)とその風速(1m/s刻み)を答えよ。
②その時刻における瞬間風速の平均風速に対する比を四捨五入により小数第1位までの数値で答えよ。
(第45回実技1、問3(4)①を改変)
①の解説:
風速の最小目盛は1(m/s)なので、0.1(m/s)まで読み取ります。
最大瞬間風速は0時50分の21.9(m/s)と読み取れるので、「1(m/s)刻み」との指示に従い22(m/s)が答えになります。
②の解説:
この時の平均風速も0.1(m/s)まで読み取り、8.9(m/s)と読み取ります。
さて、瞬間風速の平均風速に対する比を計算するときに、どの数値を使えば良いのでしょうか。
瞬間風速は21.9もしくは22、平均風速は8.9もしくは9が考えられます。①と②で有効数字が揃っていないのでこの混乱が生じます。
②では「小数第1位で答えよ」とあるので、
・計算に使う数値も小数第1位のものを使う
・途中の計算は小数第2位まで行う
・最後に小数第2位を四捨五入する
とするのが最善策です。
21.9÷8.9=2.46 →2.5となります。
ちなみに、①で1(m/s)刻みとしているので、センター発表の解答例では 22÷9=2.4 も許容されています。
センター発表解答例:
瞬間風速の平均風速に対する比: 2.5(2.4)
端数処理
端数処理とは数値を丸めることで、計算結果を最大有効桁位にするのに用いられいます。
試験では「四捨五入して答えよ」のような指示に従えば良いだけです。一般的な端数処理は四捨五入ですが、過去には「二捨三入」が出題されたことがあります。
本番でびっくりしないように慣れておきましょう。
四捨五入の問題
過去4回分(第45回〜第48回)の試験問題を分析すると、四捨五入の問題は次の二つに大別できます。
①小数第1位を四捨五入して、整数で答えさせる。
問題文としては「小数第1位を四捨五入して整数で答えよ」「四捨五入により整数値で答えよ」「四捨五入により1mm刻みで答えよ」というものです。
求める数値は整数なので、途中の計算は小数第1位まで計算し、最後に小数第1位を四捨五入して整数にします。
例) 43.5 →43
②四捨五入により小数第1位までの数値で答えさせる。
問題文としては、そのまま「四捨五入により小数第1位までの数値で答えよ」です。
小数点以下第1位までの数値を求めるので、途中の計算は小数第2位までで行います。最後に小数第2位を四捨五入して小数第1位までの数値にします。
例) 43.54 →43.5
二捨三入とは
最小の位の数字を「0」か「5」に揃えるために用いられます。
【二捨三入の処理】
端数が・・・
1・2のときは0として切り捨てる
3・4・5・6・7のときは5にする
8・9のときは10として切り上げる
端数が・・・
1・2のときは0として切り捨てる
3・4・5・6・7のときは5にする
8・9のときは10として切り上げる
この処理から「二捨三入・七捨八入」とも呼ばれます。
分かりにくいので、具体例で見てみましょう。
例)「41から50までの整数を二捨三入しなさい」
答) 41、42 → 40
43、44、45、46、47 → 45
48、49、50 → 50
二捨三入の出題事例①
最大3時間降水量を図から読み取り、二捨三入して5mm刻みで答えよ。
第45回実技2、問3(3)②(一部改変)
降水量の時系列図(ここでは省略)から最大3時間降水量は48mmもしくは49mmと読み取ることができます。
いずれの数値でも、1桁目を七捨八入をして50mmとなります。
二捨三入の出題事例②
仮温度は気温Tに水蒸気量に関する項Twを加えたものである。850hPaにおける混合比w(g/kg)からTwを求める概算式Tw=0.18wを用いて、地点aと地点bの850hPaの仮温度を求め、二捨三入により0.5℃刻みで答えよ。
第47回実技1、問2(3)②(一部改変)
この前の問題で
地点a: 気温 16.0℃、 混合比 13(g/kg)
地点b: 気温 16.0℃、 混合比 7(g/kg)
と求まっています。
有効数字は3桁として仮温度を求めます。
地点a: T=16.0+0.18×13=18.34 →18.3(小数第2位を四捨五入)
地点b: T=16.0+0.18×7=17.26 →17.3(小数2位を四捨五入)
小数第1位を二捨三入して、Ta=18.5、Tb=17.5 を得ます。
上記では小数第2位を四捨五入してから小数第1位を二捨三入するというステップを踏みました。では、小数第2位を切り捨てて小数1位を二捨三入するとどうなるでしょうか。センター発表の正解例では許容範囲になっています。
地点a: 18.34 →18.3(小数第2位を切り捨て) →18.5(小数第1位を二捨三入)
地点b: 17.26 →17.2(小数第2位を切り捨て) →17.0(小数第1位を二捨三入)
センター発表解答例:
地点a: 18.5(18.0)
地点b: 17.5(17.0、18.0)
かけ算を確実に!
そもそもですが・・・、本番の試験で計算間違いは絶対に避けなければなりません。そのためには日頃から、間違い防止を意識した計算を実践しましょう。
小手調べから
まず、次の例題を解いてみてください。
9637×3、9637×73、683×296
すんなり回答できなかったという方は、かけ算対策をすべきです。本番では検算をしている余裕はありません。一回で確実に計算できるようにしましょう。
答えは次の通りです。
9637×3=28911
9637×73=703501
683×296=202168
9637×73=703501
683×296=202168
対策
①計算は大きな字で、はっきりと書く
計算に時間をかけたくないので、用紙の隅の方に、まるで悪いことでもしているかのように書いていませんか?走り書き程度だと字がはっきりしないし、桁上がりなどを間違える可能性が高まります。
②縦の列を揃えて書くように意識する
縦の列が揃っていないと、計算の最後に同じ桁の数字を足す時に間違えが発生します。意識して列を揃えるようにします。
③繰り上がりの数字を書く
下の写真のように、繰り上がる数字を忘れないようにメモっていくやり方です。すでに実践している人も多いかと思います。
④新しい計算法を習得する
世の中にはいろんな計算法があります。「インド式」「レンガ筆算」「繰り上がり分離法」などで検索すると出てきます。いずれも③の変形法で、繰り上がる数字を明示的に書くものです。最後の足し算が長くなるというデメリットがあります。
国が異なれば計算法も異なります。気象の勉強を忘れて、計算法にのめり込みすぎないように注意!
人気ブログランキングへ
雪の防災事項 [知識]
冬季の気象情報には雪による災害に注意を促すものがあります。雪国の出身でないと分かりにくいものについてまとめてみました。
雪による主な防災事項には以下のようなものがあります。
(注)なだれと落雪に関する防災事項は省略してあります(現在、情報収集中のため)。
種類として多いのが交通障害に関するものです。その要因としては「大雪」「積雪や路面凍結」「吹きだまり」です。
交通障害とは鉄道や飛行機にあっては運休や遅延、自動車にあっては発進不能や立ち往生の発生です。
出典:HBC北海道放送
また、降雪やふぶきによる視程障害は自動車運転に支障を与えます。その他には、電線や架線、樹木などへの着雪、農作物や農業施設の被害があります。
東京出身の自分が分かりにくかったものをまとめてみました。
吹きだまりとは、雪が風に吹かれて1か所にたまったところのことです。
自動車が吹きだまりに突っ込むと雪に乗り上げてしまい、動けなくなります。また、停車中の車両の周りに吹きだまりができると発進できなくなったり、排気管が吹きだまりにより塞がれ車内に排気ガスが流入する危険があリます。
車列の先頭の車が止まってしまうと後続車が軒並みストップしてしまい、被害が拡大します。
深さ20センチの吹きだまりでも車は動けなくなると言います。近くに避難できる場所がないところで吹きだまりにはまってしまった場合は、排気ガスによる中毒防止のためにエンジンを切って車内で待ちます。
しかし、平成25年(2013年)3月、北海道で暴風雪の中、立ち往生した車の中で娘を抱きかかえたまま力尽きた父親のニュースがありました。
大雪注意報、暴風雪注意報の時はできるだけ自動車で外出しないこと、もし運転するなら防寒具、手袋、長靴、スコップを準備しておくことが大切です。
暴風に加えて雪を伴うことによる視程障害などによる重大な災害のおそれがあるとき、暴風雪警報が発表されます。
雪が舞い上がると視程障害、いわゆるホワイトアウトが発生し、数メートル先も見えなくなります。このため自動車は立ち往生してしまいます。
東日本高速道路(株)新潟支社管内の冬季の通行止めの50%以上が降雪による視程不良だと言います。
対策としては、道路防雪林や防雪柵、視線誘導施設の整備、視界情報の提供や交通規制などが行われます。
0℃前後の雪は着雪しやすく、電線にも着雪します。雪の重みで電線の切断、送電線のショート、送電鉄塔の倒壊が発生すると停電となります。
山奥で送電線が切断するとバックカントリーのスキーで入山して修理をするそうです。
出典:北海道電力
高速走行中の鉄道の車体に雪が付着すると、落下した着雪がバラスト(線路の砂利)を跳ね飛ばす危険性が高くなります。この予防として速度を落として運転するため、遅延が発生します。
農作物は茎が折れたり枯れたりして出荷できなくなるほか、畜産は換気不足が発生します。しかし、被害金額では農業施設の損害が大きいようです。
農業用施設とは農畜産物の生産、集荷、貯蔵などに使われる施設です。具体的にはハウス(ビニールハウス、パイプハウス)、育苗施設、牛舎、鶏舎、養殖施設などがあります。
積雪により施設倒壊が発生しますが、農道の除雪が進まないために全容把握と復旧には時間を要することがあります。また、生乳を集める集乳車が積雪のため回れず、廃棄を余儀なくされることもあります。
出典:京都新聞
統計によると農業施設の被害額は農作物の10倍ほどになります。対策としては冬期間に使用しない施設の撤去、補強、除雪作業に支障となる物を移動します。
参考文献:
吹雪時の視程障害度の評価に関する研究(寒地土木研究所)
http://www2.ceri.go.jp/jpn/pdf2/panf-200907-poorvisibility.pdf
北海道地方における暴風雪に対する取り組み(札幌管区気象台)
http://www.jma.go.jp/jma/kishou/books/yohkens/21/Appendix1.pdf
電線着雪災害の変遷とその研究史(北大低温科学研究所)
http://www.eng.hokudai.ac.jp/nds/311.pdf
吹雪はこんなに恐ろしい!もしもの時に身を守る方法(防災科学研究所)
http://www.nhk.or.jp/sonae/column/20131212.html
できていますか?暴風雪への備え(北海道総務部)
http://www.pref.hokkaido.lg.jp/sm/ktk/bsb/snow_p.htm
平成28年から29年冬期の大雪等による被害状況(農林水産省)
http://www.maff.go.jp/j/saigai/teion/20170111.html

人気ブログランキングへ
今回のポイント
・暴風雪やふぶきにより交通機関は大きな影響を受ける。
・着雪の重みで電線などが切断され停電が発生する。
・雪による農業施設の被害額は農作物の10倍に及ぶ。
・着雪の重みで電線などが切断され停電が発生する。
・雪による農業施設の被害額は農作物の10倍に及ぶ。
雪の防災事項
雪による主な防災事項には以下のようなものがあります。
・大雪による交通障害
・積雪や路面凍結による交通障害
・吹きだまりによる交通障害
・降雪による視程障害
・電線や架線、樹木などへの着雪
・農作物や農業施設の管理
・積雪や路面凍結による交通障害
・吹きだまりによる交通障害
・降雪による視程障害
・電線や架線、樹木などへの着雪
・農作物や農業施設の管理
(注)なだれと落雪に関する防災事項は省略してあります(現在、情報収集中のため)。
種類として多いのが交通障害に関するものです。その要因としては「大雪」「積雪や路面凍結」「吹きだまり」です。
交通障害とは鉄道や飛行機にあっては運休や遅延、自動車にあっては発進不能や立ち往生の発生です。
出典:HBC北海道放送
また、降雪やふぶきによる視程障害は自動車運転に支障を与えます。その他には、電線や架線、樹木などへの着雪、農作物や農業施設の被害があります。
東京出身の自分が分かりにくかったものをまとめてみました。
吹きだまりによる交通障害
吹きだまりとは、雪が風に吹かれて1か所にたまったところのことです。
自動車が吹きだまりに突っ込むと雪に乗り上げてしまい、動けなくなります。また、停車中の車両の周りに吹きだまりができると発進できなくなったり、排気管が吹きだまりにより塞がれ車内に排気ガスが流入する危険があリます。
車列の先頭の車が止まってしまうと後続車が軒並みストップしてしまい、被害が拡大します。
深さ20センチの吹きだまりでも車は動けなくなると言います。近くに避難できる場所がないところで吹きだまりにはまってしまった場合は、排気ガスによる中毒防止のためにエンジンを切って車内で待ちます。
しかし、平成25年(2013年)3月、北海道で暴風雪の中、立ち往生した車の中で娘を抱きかかえたまま力尽きた父親のニュースがありました。
大雪注意報、暴風雪注意報の時はできるだけ自動車で外出しないこと、もし運転するなら防寒具、手袋、長靴、スコップを準備しておくことが大切です。
降雪やふぶきによる視程障害
暴風に加えて雪を伴うことによる視程障害などによる重大な災害のおそれがあるとき、暴風雪警報が発表されます。
雪が舞い上がると視程障害、いわゆるホワイトアウトが発生し、数メートル先も見えなくなります。このため自動車は立ち往生してしまいます。
東日本高速道路(株)新潟支社管内の冬季の通行止めの50%以上が降雪による視程不良だと言います。
対策としては、道路防雪林や防雪柵、視線誘導施設の整備、視界情報の提供や交通規制などが行われます。
電線や架線、樹木などへの着雪
0℃前後の雪は着雪しやすく、電線にも着雪します。雪の重みで電線の切断、送電線のショート、送電鉄塔の倒壊が発生すると停電となります。
山奥で送電線が切断するとバックカントリーのスキーで入山して修理をするそうです。
出典:北海道電力
高速走行中の鉄道の車体に雪が付着すると、落下した着雪がバラスト(線路の砂利)を跳ね飛ばす危険性が高くなります。この予防として速度を落として運転するため、遅延が発生します。
農作物や農業施設の管理
農作物は茎が折れたり枯れたりして出荷できなくなるほか、畜産は換気不足が発生します。しかし、被害金額では農業施設の損害が大きいようです。
農業用施設とは農畜産物の生産、集荷、貯蔵などに使われる施設です。具体的にはハウス(ビニールハウス、パイプハウス)、育苗施設、牛舎、鶏舎、養殖施設などがあります。
積雪により施設倒壊が発生しますが、農道の除雪が進まないために全容把握と復旧には時間を要することがあります。また、生乳を集める集乳車が積雪のため回れず、廃棄を余儀なくされることもあります。
出典:京都新聞
統計によると農業施設の被害額は農作物の10倍ほどになります。対策としては冬期間に使用しない施設の撤去、補強、除雪作業に支障となる物を移動します。
参考文献:
吹雪時の視程障害度の評価に関する研究(寒地土木研究所)
http://www2.ceri.go.jp/jpn/pdf2/panf-200907-poorvisibility.pdf
北海道地方における暴風雪に対する取り組み(札幌管区気象台)
http://www.jma.go.jp/jma/kishou/books/yohkens/21/Appendix1.pdf
電線着雪災害の変遷とその研究史(北大低温科学研究所)
http://www.eng.hokudai.ac.jp/nds/311.pdf
吹雪はこんなに恐ろしい!もしもの時に身を守る方法(防災科学研究所)
http://www.nhk.or.jp/sonae/column/20131212.html
できていますか?暴風雪への備え(北海道総務部)
http://www.pref.hokkaido.lg.jp/sm/ktk/bsb/snow_p.htm
平成28年から29年冬期の大雪等による被害状況(農林水産省)
http://www.maff.go.jp/j/saigai/teion/20170111.html
人気ブログランキングへ